60. The Permanent Income Model#
Contents
60.1. Overview#
This lecture describes a rational expectations version of the famous permanent income model of Milton Friedman [Friedman, 1956].
Robert Hall cast Friedman’s model within a linear-quadratic setting [Hall, 1978].
Like Hall, we formulate an infinite-horizon linear-quadratic savings problem.
We use the model as a vehicle for illustrating
alternative formulations of the state of a dynamic system
the idea of cointegration
impulse response functions
the idea that changes in consumption are useful as predictors of movements in income
Background readings on the linear-quadratic-Gaussian permanent income model are Hall’s [Hall, 1978] and chapter 2 of [Ljungqvist and Sargent, 2018].
Let’s start with some imports
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (11, 5) #set default figure size
import numpy as np
import random
from numba import jit
60.2. The Savings Problem#
In this section, we state and solve the savings and consumption problem faced by the consumer.
60.2.1. Preliminaries#
We use a class of stochastic processes called martingales.
A discrete-time martingale is a stochastic process (i.e., a sequence of random variables)
Here
The latter is just a collection of random variables that the modeler declares
to be visible at
When not explicitly defined, it is usually understood that
Martingales have the feature that the history of past outcomes provides no predictive power for changes between current and future outcomes.
For example, the current wealth of a gambler engaged in a “fair game” has this property.
One common class of martingales is the family of random walks.
A random walk is a stochastic process
for some IID zero mean innovation sequence
Evidently,
Not every martingale arises as a random walk (see, for example, Wald’s martingale).
60.2.2. The Decision Problem#
A consumer has preferences over consumption streams that are ordered by the utility functional
where
The consumer maximizes (60.1) by choosing a consumption, borrowing plan
Here
The consumer also faces initial conditions
60.2.3. Assumptions#
For the remainder of this lecture, we follow Friedman and Hall in assuming that
Regarding the endowment process, we assume it has the state-space representation
where
The spectral radius of
The restriction on
Regarding preferences, we assume the quadratic utility function
where
Note
Along with this quadratic utility specification, we allow consumption to be negative. However, by choosing parameters appropriately, we can make the probability that the model generates negative consumption paths over finite time horizons as low as desired.
Finally, we impose the no Ponzi scheme condition
This condition rules out an always-borrow scheme that would allow the consumer to enjoy bliss consumption forever.
60.2.4. First-Order Conditions#
First-order conditions for maximizing (60.1) subject to (60.2) are
These optimality conditions are also known as Euler equations.
If you’re not sure where they come from, you can find a proof sketch in the appendix.
With our quadratic preference specification, (60.5) has the striking implication that consumption follows a martingale:
(In fact, quadratic preferences are necessary for this conclusion 1.)
One way to interpret (60.6) is that consumption will change only when “new information” about permanent income is revealed.
These ideas will be clarified below.
60.2.5. The Optimal Decision Rule#
Now let’s deduce the optimal decision rule 2.
Note
One way to solve the consumer’s problem is to apply dynamic programming as in this lecture. We do this later. But first we use an alternative approach that is revealing and shows the work that dynamic programming does for us behind the scenes.
In doing so, we need to combine
the optimality condition (60.6)
the period-by-period budget constraint (60.2), and
the boundary condition (60.4)
To accomplish this, observe first that (60.4) implies
Using this restriction on the debt path and solving (60.2) forward yields
Take conditional expectations on both sides of (60.7) and use the martingale property of consumption and the law of iterated expectations to deduce
Expressed in terms of
where the last equality uses
These last two equations assert that consumption equals economic income
financial wealth equals
non-financial wealth equals
total wealth equals the sum of financial and non-financial wealth
a marginal propensity to consume out of total wealth equals the interest factor
economic income equals
a constant marginal propensity to consume times the sum of non-financial wealth and financial wealth
the amount the consumer can consume while leaving its wealth intact
60.2.5.1. Responding to the State#
The state vector confronting the consumer at
Here
Note that
It is plausible that current decisions
This is indeed the case.
In fact, from this discussion, we see that
Combining this with (60.9) gives
Using this equality to eliminate
To get from the second last to the last expression in this chain of equalities is not trivial.
A key is to use the fact that
We’ve now successfully written
60.2.5.2. A State-Space Representation#
We can summarize our dynamics in the form of a linear state-space system governing consumption, debt and income:
To write this more succinctly, let
and
Then we can express equation (60.11) as
We can use the following formulas from linear state space models to compute population mean
We can then compute the mean and covariance of
60.2.5.3. A Simple Example with IID Income#
To gain some preliminary intuition on the implications of (60.11), let’s look at a highly stylized example where income is just IID.
(Later examples will investigate more realistic income streams.)
In particular, let
Finally, let
Under these assumptions, we have
Further, if you work through the state space representation, you will see that
Thus, income is IID and debt and consumption are both Gaussian random walks.
Defining assets as
The next figure shows a typical realization with
r = 0.05
β = 1 / (1 + r)
σ = 0.15
μ = 1
T = 60
@jit
def time_path(T):
w = np.random.randn(T+1) # w_0, w_1, ..., w_T
w[0] = 0
b = np.zeros(T+1)
for t in range(1, T+1):
b[t] = w[1:t].sum()
b = -σ * b
c = μ + (1 - β) * (σ * w - b)
return w, b, c
w, b, c = time_path(T)
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(μ + σ * w, 'g-', label="Non-financial income")
ax.plot(c, 'k-', label="Consumption")
ax.plot( b, 'b-', label="Debt")
ax.legend(ncol=3, mode='expand', bbox_to_anchor=(0., 1.02, 1., .102))
ax.grid()
ax.set_xlabel('Time')
plt.show()
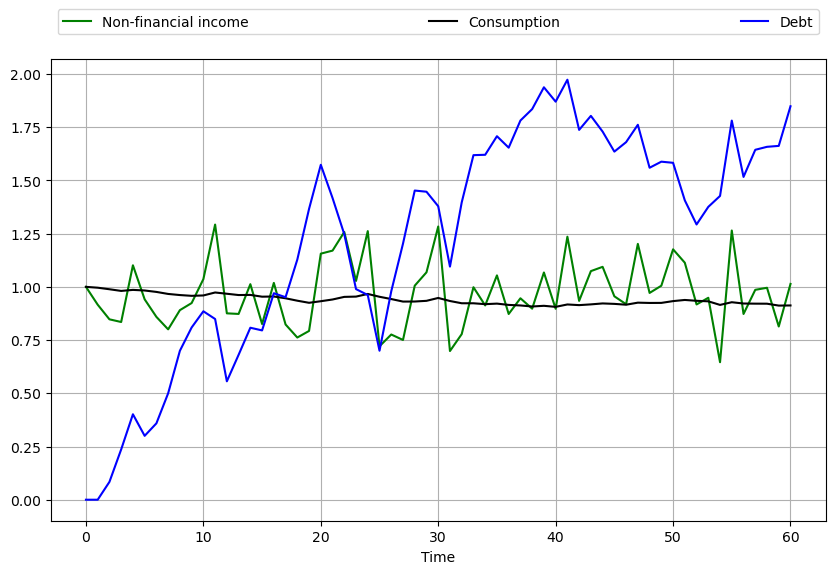
Observe that consumption is considerably smoother than income.
The figure below shows the consumption paths of 250 consumers with independent income streams
fig, ax = plt.subplots(figsize=(10, 6))
b_sum = np.zeros(T+1)
for i in range(250):
w, b, c = time_path(T) # Generate new time path
rcolor = random.choice(('c', 'g', 'b', 'k'))
ax.plot(c, color=rcolor, lw=0.8, alpha=0.7)
ax.grid()
ax.set(xlabel='Time', ylabel='Consumption')
plt.show()
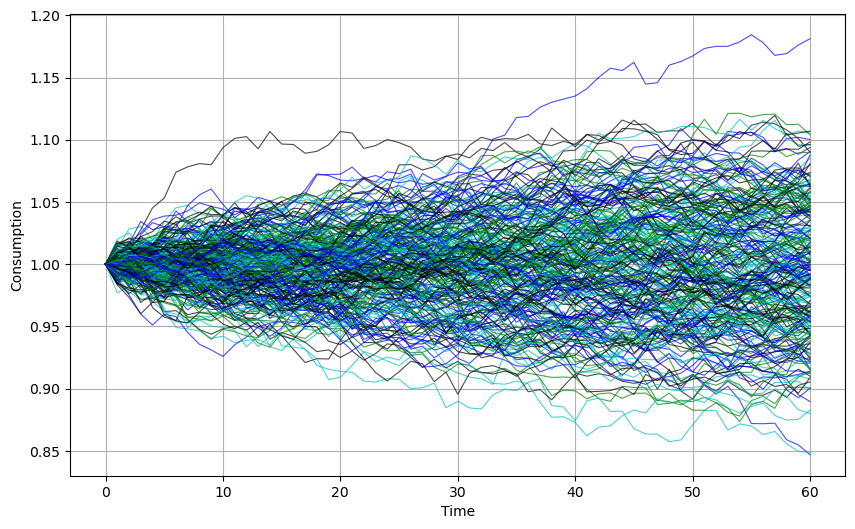
60.3. Alternative Representations#
In this section, we shed more light on the evolution of savings, debt and consumption by representing their dynamics in several different ways.
60.3.1. Hall’s Representation#
Hall [Hall, 1978] suggested an insightful way to summarize the implications of LQ permanent income theory.
First, to represent the solution for
If we add and subtract
The right side is the time
We can represent the optimal decision rule for
Equation (60.17) asserts that the consumer’s debt due at
A high debt thus indicates a large expected present value of surpluses
Recalling again our discussion on forecasting geometric sums, we have
Using these formulas together with (60.3) and substituting into (60.16) and (60.17) gives the following representation for the consumer’s optimum decision rule:
Representation (60.18) makes clear that
The state can be taken as
The endogenous part is
Debt
Consumption is a random walk with innovation
This is a more explicit representation of the martingale result in (60.6).
60.3.2. Cointegration#
Representation (60.18) reveals that the joint process
Cointegration is a tool that allows us to apply powerful results from the theory of stationary stochastic processes to (certain transformations of) nonstationary models.
To apply cointegration in the present context, suppose that
Despite this, both
Nevertheless, there is a linear combination of
In particular, from the second equality in (60.18) we have
Hence the linear combination
Accordingly, Granger and Engle would call
When applied to the nonstationary vector process
Equation (60.19) can be rearranged to take the form
Equation (60.20) asserts that the cointegrating residual on the left side equals the conditional expectation of the geometric sum of future incomes on the right 4.
60.3.3. Cross-Sectional Implications#
Consider again (60.18), this time in light of our discussion of distribution dynamics in the lecture on linear systems.
The dynamics of
or
The unit root affecting
In particular, since
where
When
Let’s consider what this means for a cross-section of ex-ante identical consumers born at time
Let the distribution of
Equation (60.22) tells us that the variance of
A number of different studies have investigated this prediction and found some support for it (see, e.g., [Deaton and Paxson, 1994], [Storesletten et al., 2004]).
60.3.4. Impulse Response Functions#
Impulse response functions measure responses to various impulses (i.e., temporary shocks).
The impulse response function of
In particular, the response of
60.3.5. Moving Average Representation#
It’s useful to express the innovation to the expected present value of the endowment process in terms of a moving average representation for income
The endowment process defined by (60.3) has the moving average representation
where
Notice that
It follows that
Using (60.24) in (60.16) gives
The object
60.4. Two Classic Examples#
We illustrate some of the preceding ideas with two examples.
In both examples, the endowment follows the process
Here
60.4.1. Example 1#
Assume as before that the consumer observes the state
In view of (60.18) we have
Formula (60.26) shows how an increment
a permanent one-for-one increase in consumption and
no increase in savings
But the purely transitory component of income
The remaining fraction
Application of the formula for debt in (60.11) to this example shows that
This confirms that none of
The next figure displays impulse-response functions that illustrates these very different reactions to transitory and permanent income shocks.
r = 0.05
β = 1 / (1 + r)
S = 5 # Impulse date
σ1 = σ2 = 0.15
@jit
def time_path(T, permanent=False):
"Time path of consumption and debt given shock sequence"
w1 = np.zeros(T+1)
w2 = np.zeros(T+1)
b = np.zeros(T+1)
c = np.zeros(T+1)
if permanent:
w1[S+1] = 1.0
else:
w2[S+1] = 1.0
for t in range(1, T):
b[t+1] = b[t] - σ2 * w2[t]
c[t+1] = c[t] + σ1 * w1[t+1] + (1 - β) * σ2 * w2[t+1]
return b, c
fig, axes = plt.subplots(2, 1, figsize=(10, 8))
titles = ['permanent', 'transitory']
L = 0.175
for ax, truefalse, title in zip(axes, (True, False), titles):
b, c = time_path(T=20, permanent=truefalse)
ax.set_title(f'Impulse reponse: {title} income shock')
ax.plot(c, 'g-', label="consumption")
ax.plot(b, 'b-', label="debt")
ax.plot((S, S), (-L, L), 'k-', lw=0.5)
ax.grid(alpha=0.5)
ax.set(xlabel=r'Time', ylim=(-L, L))
axes[0].legend(loc='lower right')
plt.tight_layout()
plt.show()
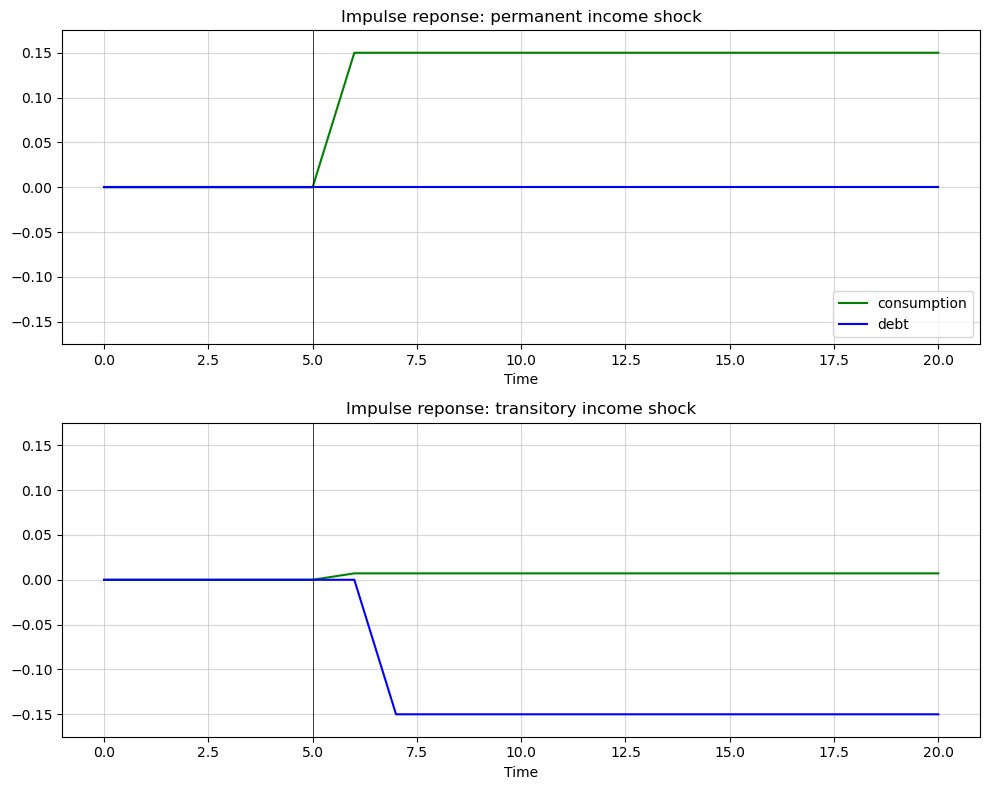
Notice how the permanent income shock provokes no change in assets
In contrast, notice how most of a transitory income shock is saved and only a small amount is saved.
The box-like impulse responses of consumption to both types of shock reflect the random walk property of the optimal consumption decision.
60.4.2. Example 2#
Assume now that at time
Under this assumption, it is appropriate to use an innovation representation to form
The discussion in sections 2.9.1 and 2.11.3 of [Ljungqvist and Sargent, 2018] shows that the pertinent state space representation for
where
In the same discussion in [Ljungqvist and Sargent, 2018] it is shown that
In other words,
Please see first look at the Kalman filter.
Applying formulas (60.18) implies
where the endowment process can now be represented in terms of the univariate innovation to
Equation (60.29) indicates that the consumer regards
fraction
fraction
The consumer permanently increases his consumption by the full amount of his estimate of the permanent part of
Therefore, in total, he permanently increments his consumption by a fraction
He saves the remaining fraction
According to equation (60.29), the first difference of income is a first-order moving average.
Equation (60.28) asserts that the first difference of consumption is IID.
Application of formula to this example shows that
This indicates how the fraction
60.5. Further Reading#
The model described above significantly changed how economists think about consumption.
While Hall’s model does a remarkably good job as a first approximation to consumption data, it’s widely believed that it doesn’t capture important aspects of some consumption/savings data.
For example, liquidity constraints and precautionary savings appear to be present sometimes.
Further discussion can be found in, e.g., [Hall and Mishkin, 1982], [Parker, 1999], [Deaton, 1991], [Carroll, 2001].
60.6. Appendix: The Euler Equation#
Where does the first-order condition (60.5) come from?
Here we’ll give a proof for the two-period case, which is representative of the general argument.
The finite horizon equivalent of the no-Ponzi condition is that the agent
cannot end her life in debt, so
From the budget constraint (60.2) we then have
Here
Substituting these constraints into our two-period objective
You will be able to verify that the first-order condition is
Using
The proof for the general case is similar.
- 1
A linear marginal utility is essential for deriving (60.6) from (60.5). Suppose instead that we had imposed the following more standard assumptions on the utility function:
- 2
An optimal decision rule is a map from the current state into current actions—in this case, consumption.
- 3
This would be the case if, for example, the spectral radius of
- 4
See [John Y. Campbell, 1988], [Lettau and Ludvigson, 2001], [Lettau and Ludvigson, 2004] for interesting applications of related ideas.
- 5
Representation (60.3) implies that
- 6
A moving average representation for a process